連立 不等式 a の とり うる 値 の 範囲

うぐいす や 旅館 ペット連立不等式の解き方!共通範囲の求め方も図で即理解!文章題 . 1：連立不等式の解き方①：共通範囲もよく分かる! まず、連立不等式の解き方について例題をあげて解説していきます。 例題 次の不等式を同時に満たすxの範囲を求めなさい。 5x+2<2x+14・・・① 8x-10≧5x-16・・・② 解答＆解説. 連立不等式を解くコツを徹底解説!!! - 理数白書. 分解して連立不等式を立てるのが鉄則です。 $begin{eqnarray}left{begin{array}{1}2x+6<3x+83x+8<5x+2end{array}right.end{eqnarray}$ こういうふうに分解するんです。そうすれば今まで解いてきた連立不等式と同じノリで解くことが. とりうる値の範囲(数I・A)を教えてください -<問題>連立不等式 7x . 1-3aが4以下であれば、連立不等式の解に4がふくまれることになります。 そのため、1-3aは4より大となります。 また、1-3aが5以下でないと、連立不等式の解に5がふくまれなくなります。. 連立不等式の解き方を解説!数直線の書き方、絶対値の問題も . 連立不等式の解は、連立しているすべての不等式の範囲が重なる部分です。 数直線上で①と②が重なる部分に色をつけてみましょう。 この共通範囲が、この連立不等式の解になります。. 連立不等式の解き方を7枚の画像で図解!共通範囲の求め方から . この連立不等式の解（①と②の共通範囲）は次の通り。 $$-5<x≦1$$ これを数直線に表すと、 連立不等式を解く上で、「数直線」の概念はとても重要になります。. 「連立不等式を満たす整数解の個数からaの範囲を求める」の . 【動画で解説】連立不等式 x＞3a＋1，2xー1＞6 (xー2) を満たす解が存在しないような，定数aの値の範囲を求める（1130 高校数学） 解説くん「数学」 3K views 2 years ago. 重複組合せ Lv.3. はやくち解説高校数学. 13K views 5 years ago. 【3分で分かる!】連立不等式の解き方をわかりやすく - 合格 . 二次不等式の問題の解答・解説. まず、上の不等式を解きます。. 因数分解 をして、 (2x + 1)(x − 3) < 0. A×B<0 ⇔ 「A<0かつB>0、またはA>0かつB<0」であることを、ここで用いると. 「2x + 1 < 0かつx − 3 > 0、または2x + 1 > 0かつx − 3 < 0」. よって、「 x < −12 . 不等式の解き方まとめ!高校数学はこれでバッチリ! - 数スタ. （2）不等式(8-2x<2x<x+a)を満たす整数(x)がちょうど4個存在するとき、(a)の値の範囲を求めよ。 まずは、連立不等式を作って解を求めてみましょう。. 数学Ⅰ｜数直線を用いた連立不等式の解の求め方とコツ | 教科 . 共通範囲より、解は −1 ≦ x < 3 となる. また、 x ≧ −1 かつ x > 3 では、 共通範囲より、解は x > 3 となる. A < B < C の連立不等式. {A < B B < C. このように、 2つの1次不等式に分けて、連立不等式として計算できる 。 ©︎ 2024 教科書より詳しい高校数学 yorikuwa.com. 次のページ「解法のPointと問題解説」 次へ. 1. 数学Ⅰ：数と式. 連立不等式の解の求め方を解説していきます。 解法の手順は、1次不等式の解を求めて数直線上に範囲を表し共通範囲を求めましょう。. 連立不等式の解の求め方｜数学｜苦手解決q&A｜進研ゼミ . 連立不等式の解は、それぞれの不等式の解の範囲を数直線で表し、それらの共通範囲を求めます。 「3< x かつ x <5の共通範囲は3< x <5」のように2つの値に挟まれる場合はわかりやすいのですが、今回のように「2< x かつ 5< x 」のように不等号の向きが同じ場合は注意が必要です。 数直線の見方をしっかりマスターしましょう。 それでは、これで回答を終わります。 これからも『進研ゼミ高校講座』にしっかりと取り組んでいってくださいね。. 連立不等式の簡単な問題とその解き方 - マナペディア. …②. とりあえず、①と②の不等式をそれぞれ解いてみましょう。 【①の不等式】 …③. 【②の不等式】 …④. ①の不等式におけるxの範囲が. ②の不等式におけるxの範囲が となりました。 これを図に表してみましょう。 図を見れば一目瞭然ですね。 ③と④の範囲でかぶっているところが今回求めるべきxの範囲になります。 連立不等式で、xの範囲を求めよという問題であれば、今回のように2つの不等式で、それぞれのxの範囲を求めて、かぶっているところを求めなさいということです。 ・ 不等式の基本とその解き方. ・ 高校数学Ⅰで使う不等式の性質・計算方法. ・ 不等式を計算するときに覚えておきたい法則・性質. ・ 1次不等式の解き方 [カッコ・分数・少数を含む1次不等式の問題]. 【連立不等式の整数解】範囲に「＝」をつける、つけない . 連立不等式の整数解とは、次のような問題のことをいいます。 【問題】ニューアクションβより. a を定数とする。 2つの不等式. 2(3x − 4) − 1 > −3(2x + 11) ⋯①. 4x + 2a < 3x + 2 ⋯②. をともに満たす整数 x がちょうど3個となるような a の値を求めよ。 よく聞かれる質問として、 答えの範囲に＜、≦のどちらを選べばいいか分かりません… というものがあります。 というわけですので、 この点について詳しく解説していきますね! 今回の内容をサクッと学びたい方は、こちらの動画をチェック! Contents. 連立不等式の整数解の問題解説! 練習問題に挑戦! まとめ! 連立不等式の整数解の問題解説! 【問題】ニューアクションβより. a を定数とする。. 【数学ia】2次不等式を含む連立不等式 | 大学入試数学の考え方 . hiroをフォローする. ここでは2次不等式を含む連立不等式の解き方を説明します。 「連立」と付いても連立方程式のように未知数が複数あるわけではなく，未知数は1つです。 複数の不等式を満たす未知数の値の範囲を求めるだけです。 連立不等式を解くこと自体は少しの練習で出来るよ. 【連立不等式】3つの不等式の解き方を問題解説! - 数スタ. 【連立不等式】3つの不等式の解き方を問題解説! LINE. 今回は高校数学Ⅰで学習する. 『不等式』という単元から. こういった問題の解き方を解説していきます。 −8 < 3x − 5 < 4. 3つの式がつながっている不等式! これはどのように解いていけば良いのでしょうか。 Contents. 3つの不等式の解き方. 演習問題で理解を深める! 3つの不等式解き方 まとめ. 3つの不等式の解き方. 次の不等式を解け。 −8 < 3x − 5 < 4. このように3つの式がつながっている不等式を解くためには. 2つの不等式に分けて、連立不等式として解いていきます。 3つの不等式のうち. 小＜中＜大. ⇒ 小＜中. ⇒ 中＜大. というように2つの不等式にわけます。. 数と式|連立不等式の解の求め方|数学Ⅰ|定期テスト対策サイト. 連立不等式の解は、それぞれの不等式の解の範囲を数直線で表し、それらの共通範囲を求めます。 「3< x かつ x <5の共通範囲は3< x <5」のように2つの値に挟まれる場合はわかりやすいのですが、今回のように「2< x かつ 5< x 」のように不等号の向きが同じ場合は注意が必要です。 数直線の見方をしっかりマスターしましょう。. 中等教育前期の数学/代数編/上巻/一次不等式と連立不等式 . いくつかの不等式を組み合わせたものを 連立不等式 といい、これらの不等式を同時に満たす の値の範囲を求めることを、連立不等式を 解く という。. 【動画で解説】連立不等式 x＞3a＋1，2xー1＞6(xー2) を . 3K views 2 years ago 数学Ⅰ 1次不等式・絶対値. ★説明がわかりやすい!. と思っていただけたら 「高評価」＆「チャンネル登録」お願いします!. ★ . 連立2次不等式. 連立2次不等式. それぞれの不等式を解いて、共通の範囲を求める。 { x2−x−6<0 x2+6x+5≧0. { x2−x−6<0・・・① x2+6x+5≧0・・・②. ①を解くと−2<x<3. 願望実現オフィス 能力に目覚めた男 東條なつ

ゲーミング チェア で 寝る②を解くとx≦−5, −1≦x. 両方を数直線に表すと x -5 -2 -1 3 ① ② ②.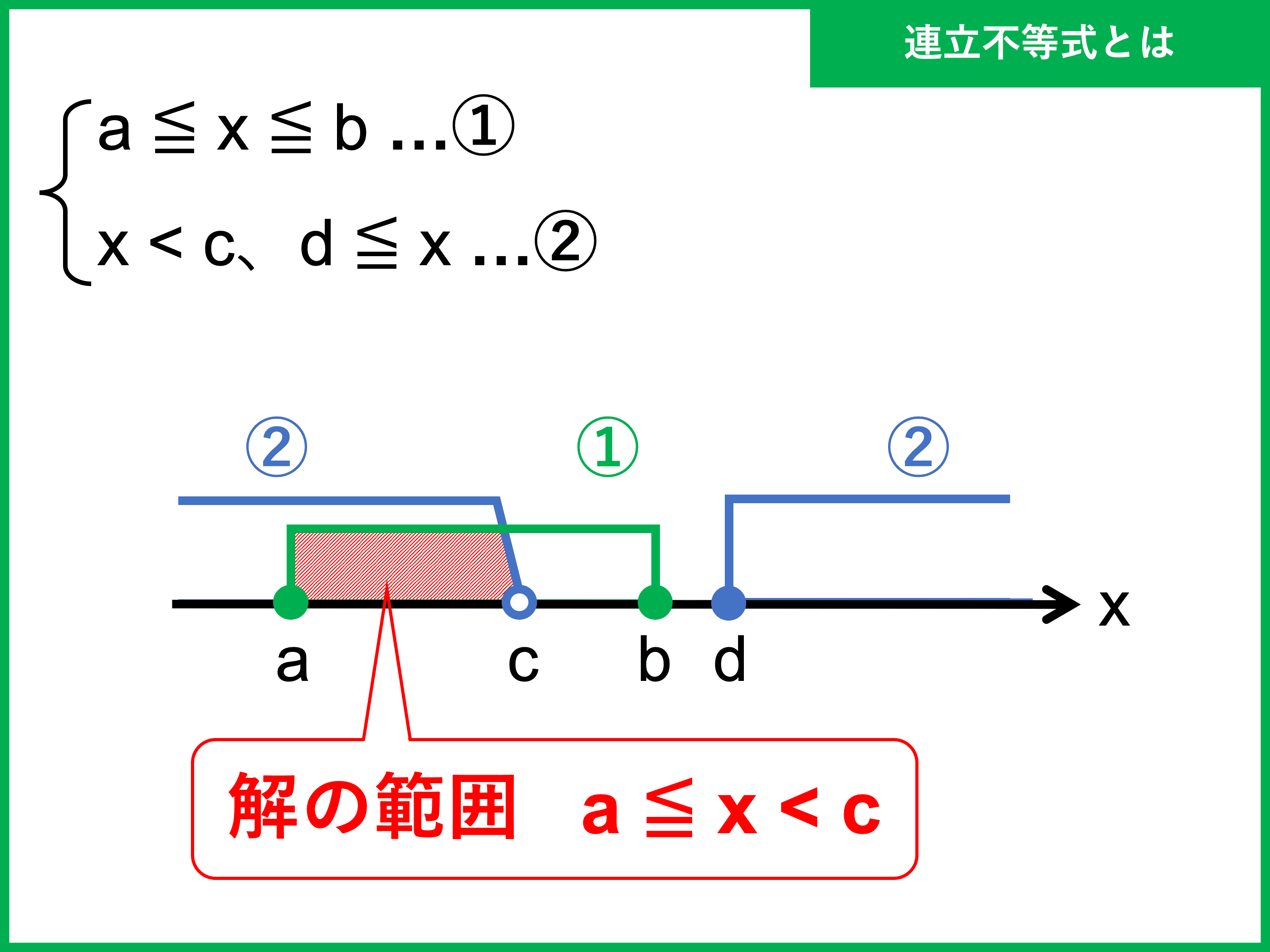

よって共通範囲は −1≦x<3. { x2-5x+4>0 x2-2x-15≦0 { x2+3x-4<0 x2-x-6≦0 { x2+x-6>0 x2-3x-4>0. 答表示. 不等式の式の値の範囲 | すうがくのいえ. 不等式の問題で「式の値の範囲」を問われることがある。 不等式の性質 を使うことで、 「式の値の範囲」 を答える問題を解くことができる。 合わせて不等式の計算に使える法則も確認する。. 【高校数学Ⅰ】不等式の基本性質と式の値の範囲 | 受験の月. 不等式の基本性質と式の値の範囲. 2019.06.23. 検索用コード. 不等号の盲点 2つの実数$a, b$に対し, $a>b, a=b, a b}$ {ま} {た} {は}$ {a=b}$}」}を意味する ($a>b$かつ$a=b$はありえない). つまり, $a>b$と$a=b$のどちらか一方が成り立てば, $a b$は正しい不等式である. よって, $10$はもちろん ($1>0$が成り立つ), $00$も正しい不等式}である. $0>0$は成り立たないが, $0=0$が成り立つからである. 連立不等式 aの取りうる値の範囲について教えて下さい。 -←の . 連立不等式 aの取りうる値の範囲について教えて下さい。 解決済. 気になる. 件. 質問者： mellbell. 質問日時： 2021/05/30 08:41. 回答数： 1 件. ←の部分なのですが、0＜a+2≦1 でa+2=1だった場合、-2, -1,0,1の4個含まれるので混乱しています…。 私は、0≦a+2＜1だと思っているのですがご教授お願いします。 通報する. この質問への回答は締め切られました。 質問の本文を隠す. A 回答 (1件) ベストアンサー優先.

最新から表示. 猫 の ノミ 取り 意味

屋 我 地島 の 塩回答順に表示. No.1 ベストアンサー. 回答者： mtrajcp. 回答日時： 2021/05/30 09:25. 0<a+2≦1 でa+2=1だった場合. a=-1. だから. 【高校数学Ⅱ】実数解のとりうる値の範囲（逆像法） | 受験の月. (1) $x^2-2ax+2a^2-4=0$の実数解$x$のとりうる値の範囲を求めよ. (2) $0≦ a≦2 のとき, x^2-2ax+2a^2-4=0$の実数解$x$のとりうる値の範囲を {実数解のとりうる値の範囲 (1) $a$で整理すると$a$の方程式①が実数解をもつよう. 【数学講師向け】不等式の基本をおさえるー不等式の意味 . 2021/12/17. 不等式の意味とは？ 不等式には大きく分けて3つの意味があります。 ・単なる大小関係を表す時に使う. ・解集合を表す. ・取りうる値の範囲を表す. ・大小関係. 例えば、a≧bは a>bまたはa=b の少なくとも一方が成り立つと主張しているだけです。 したがって、3>1と3≧1のうち、正しいのはどれか？ という問題を出したときの答えは「どちらも正しい」となります。 ・解集合. x^2-3x+2=0 を解くとxは1と2となり、 {1,2}という解集合が求められます。 「=」を変えて「<」とすると、 x^2-3x+2<0 となり、xの解は1<x<2となり、1<x<2を満たすx全体が解となります。 詳しくは後ほど例題①を参照してください。 ・取り得る値の範囲.

うさぎでもわかる解析 Part12 2変数関数の定義域・値域・図示 | 工業大学生ももやまのうさぎ塾. 6．さいごに. 今回は2変数関数についての基礎的な知識として2変数関数の定義域・値域、2変数関数の図示（というか想像）の仕方についてまとめました。. 2変数関数の図示の方法は様々な方法があるので参考までにしてください。. *1:書いていませんが 9 = 3 . とりうる値の範囲(数i・A)を教えてください| Okwave. とりうる値の範囲. 不等式2(x+a)<3(1-x)について次の問いに答えよ。 (1) 解がx<3となるように、定数aの値を定めよ。 (2) 解がx=(-3)を含まないように、定数aの値の範囲を定めよ。 答え (1) a=(-6) (2) a≧9 になるそうです 解き方の解説よろしくお願いします。. 二次不等式とは？解き方や解の範囲の求め方、判別式の問題 | 受験辞典. この記事では、「二次不等式」の定義や解の範囲の求め方をできるだけわかりやすく解説していきます。 また、判別式を利用した問題の解き方なども紹介していきますので、この記事を通してぜひマスターしてくださいね。 目次二次不等 .

不等式の性質 | 教えて数学理科. 不等式には以下の性質があります。. ②は a > b は、天秤の片方に a 、もう一方に b が乗っていて傾いているイメージです。. 両方に同じ数を足したり引いたりしても傾きは変わりません。. ③ (A)も同様です。. 同じ数 (ただし正の数)で掛けたり割ったりしても . 絶対値を含む不等式の解き方まとめ | 理系ラボ. 東大塾長の山田です。 このページでは、「絶対値を含む不等式の解き方」について解説します。 「絶対値記号のはずし方の基本」からしっかり解説しつつ、具体的に問題を解きながら、「絶対値を含む不等式の解き方」を、丁寧に分かりやすく解説しています。. t=sinθ+cosθとし、tの取りうる値の範囲を求めると合成よりt＝. - Yahoo!知恵袋. 教養と学問、サイエンス. 数学. やまびこ さん. 2013/3/3 10:03. 1 回答. t=sinθ+cosθとし、tの取りうる値の範囲を求めると 合成よりt＝√2sin (θ+π/4) -1≦sin (θ+π/4)≦1 -√2≦t≦√2となりますが、この±√2はどのようにして求めたのでしょうか？. 数学 ・ 11,793 閲覧. 1 . 取り得る値の範囲？ - 実数x,yがx^2-2xy+2y^2=2. - Yahoo!知恵袋. 高1物理基礎、波の問題です。. この問題の解き方を教えていただきたいです。. 答えは、 (1)L/t₂-v [m/s] (2)t₁L/t₂ [m] (3)L-vt₂/Lt₁ [Hz] です!. bbb 大きな 乳 とお 尻 3 黒木 あおい

可憐 な 妻たち 宇都宮ご回答お待ちしております。. 取り得る値の範囲？. 実数x,yがx^2-2xy+2y^2=2を満たすとき、2x+yの取り得る値の範囲を . 高次方程式の実数解のとりうる範囲 | 教えて数学理科. 高次方程式の実数解のとりうる範囲. 高次方程式の実数解の存在範囲に関する問題について見ていきます。. 2次関数のときと同じようにグラフを書いて、 x 軸との共有点を考えたり、文字定数を分離してグラフとの共有点の x 座標を検討します。. (例題1) 3次 . 相関係数 r の範囲は－1以上1以下であることの証明 | 岩井の数学ブログ. 相関係数 r の値の範囲は－1以上1以下になります。 高一の統計分野で学習する事実ですが、有名な不等式を利用して、証明ができます。 標準偏差と共分散を用いて定義される相関係数の範囲を示すことは、証明問題の良い練習になるかと思います。. 三角比の符号と値の範囲 | 教えて数学理科. 三角比の値は、円の半径の大きさによらず角度だけで決まるので、半径1の単位円について考えていきます。. 図のように、 となるような点 が単位円の周上にあるとき、三角比の定義より. となります。. つまり は点 の 座標、 は 座標となります。. 角度 が . 実数解がとりうる値の範囲 -0<a<2の範囲で、xについての方程式A：x^- | OKWAVE. 0<a<2の範囲で、xについての方程式A：x^2-2ax-2x+2a^2-6=0の実数解がとりうる値の範囲を求めよ。 という問題なんですが、解き方がいまいちわかりません。 ヒントには「解と係数の関係を利用し図形的に解く」や別解として「aの方程式とみる」とありました。. 同値を制する者、受験数学を制する[14.とりうる値の範囲] - YouTube. 演習の解答kmath.net/?p=2611最大値と最小値，とりうる値の範囲outu.be/nJ1CwGp3QPo＝＝＝＝＝数学の解説動画を公開し . 式の値の範囲 - UsaLabo | 中学・高校学習サイト. このサイトは中学・高校生を対象とした学習サイトです。日々の学習の中での疑問点や、予習復習などに活用してください。 また、掲載内容には十分注意を払っておりますが、全てを鵜呑みにせずに主体的に学習することを心がけてください。. 宵 の 嫁入り ネタバレ

つまらない 男 の 定番 デート高1数学です。問題に｢とりうる値を求めよ｣とあるのですが、と. - Yahoo!知恵袋. 「aのとりうる値を求めよ」のような問題でしょうか。 それでしたら、aの値はなんですかという意味かと。ただ、aが変数の場合(aが動いたりして、色々な場合が考えられるとき)は変域(3<a<5)を問われているのかもしれません。. 領域における最大最小. 上の問題では，ある直線 y=x+k が通っている点が1つでもあれば，その k の値は領域内でとれる値となり，通るべき点は2つも3つもいらないことに注意. 実際には，最大値 k=2 となる点は (0, 2) の1点だけであり，最小値 k=−2 となる点は (2, 0) の1点だけであるが . 数学Ⅰ 条件つきの式のとりうる値の範囲-基本類題35 - YouTube. #数電#数学#2次関数#とりうる値の範囲#条件つき条件つきの式のとりうる値の範囲を求める問題です。数学の問題の解き方、考え方は、何通りも . 【高校数学Ⅰ】「「平均値」と「平均値のとりうる値」」 | 映像授業のTry IT (トライイット). 今回は 「平均値」 と 「平均値のとりうる範囲」 について学習しよう。. 「平均」って、聞いたことあるよね。. 「テストの平均点は~」みたいな話で、よく出てくるよね。. 「平均値」は、式にすると次のよう求められるよ。. （平均値）＝（データの合計 . 【3分で分かる!】三角関数の不等式の解き方をわかりやすく - 合格サプリ. 三角関数sinθを含む不等式の解き方①：sinθ=aを満たす角度を求める. 不等式を解く上で最初にやることは、不等式を「sinθ=a」と置き換えた上でそれを満たす角度を求めることです。. て ぴあ ん 整体 院

全国 熟女 捜索 隊 田舎 に 泊まろ うsinθはy座標に対応するので単位円上でy=aと交わる点を求めると以下のよう . 変域ってなに？定義域と値域の違い | すうがくのいえ. 定義域と値域. 定義域と値域を考える中でさらに「変域」という言葉が出てくる。 この変域と定義域と値域について見ていく。. 変域ってなに？ 変域とは、変数のとりうる値の範囲のこと。 変数の領域で変域。. こんな感じのやつ。 定義域ってなに？ 関数(y=f(x))において、(x)の変域を「定義 . 【高校数学Ⅱ】等式条件つき2変数関数の最大・最小（逆像法） | 受験の月. xの方程式②が実数解をもつようなkの値の範囲}を求めればよい. わかりやすくするために, =kとおく. 2x+yの最大値・最小値を求めることは, kのとりうる値の範囲を求めることに等しい. x^2-2xy+2y^2=1を満たす実数(x, y)に対応して2x+y=kの値が定まる. 【高校数学Ⅱ】相加平均と相乗平均の大小関係の最大最小問題への応用、落とし穴と限界 | 受験の月. 実際のとりうる値の範囲が3≦ y≦4であったとしても, それは「2以上」である. 本問の場合, 「最小値2」は等号成立条件の確認で示せたが, それ以上は相加相乗では対応できない. 相加平均と相乗平均の大小関係の限界}がここにあり, 別法が必要になる. 数と式｜連立不等式について | 日々是鍛錬 ひびこれたんれん. 今回は連立不等式について学習します。. 「連立～式」と言われるものに連立方程式があります。. 連立する式が方程式から不等式に変わっただけです。. 解くときに不等式の性質を利用するので確認しながら進めていくと良いでしょう。. 目次. iphone 画面 を pc に 映す

やきそば パンマン と ニガウリ マン1. 連立不等式 . PDF 2005 方程式の解のとりうる値の範囲 - suugakujigaku.com. 2005 方程式の解のとりうる値の範囲 例題 0 以上の実数s; t がs2 +t2 = 1 をみたしながら動くとき; 方程式 4x −2(s+t)x2 +(s−t)2 = 0 の解のとる値の範囲を求めよ。 【東京大・文系】. 【高校数学Ⅰ】「「平均値」と「平均値のとりうる値」」(例題編) | 映像授業のTry IT (トライイット). Try IT（トライイット）の「平均値」と「平均値のとりうる値」の例題の映像授業ページです。Try IT（トライイット）は、実力派講師陣による永久0円の映像授業サービスです。更に、スマホを振る（トライイットする）ことにより「わからない」をなくすことが出来ます。. 【高校数学Ⅰ】2次不等式の整数解の個数 | 受験の月. 高校数学総覧. 高校数学Ⅰ 2次関数（2次方程式と2次不等式）. 学芸 大学 駅 住み やす さ

既婚 者 と キス 法律2次不等式の整数解の個数. 2次不等式の整数解の個数. 2019.06.16. 検索用コード. 連立不等式 x²-7x+10>0 & x²- (a+1)x+a0 & を満たす整数xが5個存在するような$ $定数aの値の範囲を求めよ.$ $3x²-16x+a<0$を . x≧0,y≧0,x+y=4のとき、xのとりうる値の範囲を求めよ. - Yahoo!知恵袋. 微分法の問題です。 x+3y=9、x≧0、y≧0のとき、x^2y（x2乗y）の最小値と最大値を次のようにして求めよ。 (1)x^2yをxだけの式で表せ。 (2)xのとりうる値の範囲を求めよ。 (3)x^2yの最大値、最小値と、そのときのx,yの値を求めよ。 この問題の解答解説をしてください。. 【完全版】一次関数のグラフから利用問題まで解き方まとめ!｜中学数学・理科の学習まとめサイト!. グラフを書くことで確かめることができるのですが、一次関数は常に一定の割合で増えたり、減ったりするという特徴を持っています。. なので、一次関数の変化の割合は常に一定であり、さらには傾き a と等しくなります。. これは結構大事なことなので . 数学の問題です。sinX+cosX=tのときのtの範囲の答えと解説. - Yahoo!知恵袋. t=sinx+cosx がとりうる値の範囲。 関数y=2sinxcosx+sinx+cosxについて、 tのとりうる値の範囲を求めよ。 という問題で、 -1≦sinx≦1, -1≦cosx≦1 から足しあわせて、 -2≦sinx+cosx≦2 としたのですが、間違いとされてしまいました。. 【数学Ⅱ】2変数関数のとりうる値の範囲 220126 - YouTube. 雇用 契約 を 結ば ない 副業

浄化 の 重 撃#入試問題解いてみた #横浜国大数学 2020点(x,y)、領域内すべてを動かして mx+y の値のとりうる値の範囲を考えます。よくあるのは mx+y=k とおいて . 【高校数学Ⅰ】2次方程式の解の存在範囲(解の配置)の基本 | 受験の月. 高校数学総覧. 高校数学Ⅰ 2次関数（2次方程式と2次不等式）. 2次方程式の解の存在範囲 (解の配置)の基本：「判別式」「軸の位置」「区間の端のy座標の正負」に着目せよ!. 2次方程式の解の存在範囲 (解の配置)の基本：「判別式」「軸の位置」「区間の端の . 三角関数の合成とは？公式と証明、範囲つき最大最小の問題 | 受験辞典. 三角関数. 三角関数の合成とは？. 公式と証明、範囲つき最大最小の問題. 2021年12月28日. ※本ページは広告を含む場合がございます. この記事では、「三角関数の合成」の公式や証明、実際のやり方をわかりやすく解説していきます。. 角度の範囲に応じて . 【高校数学Ⅱ】三角方程式の解の存在条件 | 受験の月. に2つの実数解(重解を含む)をもつ}とき$ sin^2θ+cos^2θ=1を用いて関数をsinθ,に統一し, 置換する. 置換したとき, 置換後の文字のとりうる値の範囲を確認しなければならない}ことに注意する. 特に,θ,の範囲がなければ, t=sinθ,のとりうる値の範囲は当然-1 . 連立不等式x<62x+3≧x+aの解について、次の条件を満たす. - Yahoo!知恵袋. 連立不等式x<62x+3≧x+aの解について、次の条件を満たす定数aの値の範囲を求めよ。⑴解をもつ⑵解に整数がちょうど2個含まれる。という問題なのですが、まず各不等式を解くということは 理解できました。⑴解をもつということは、具体的にどういうことでしょうか？式中のaの値を求めると . 次の式のとりうる値の範囲を求めよ。(1)～(4)では0°≦θ≦180°. - Yahoo!知恵袋. 0°≦θ≦180°のとき－2sinθ＋1のとりうる値の範囲は － ≦－2sinθ＋1≦ である。 の中に数字が入るみたいなんですが・・・ 解ける方よろしくおねがいします。. 【質問】高校数Ⅰ：連立不等式 3x+a＞6x－2, －2x+10≦x+a を満たす… | オンライン無料塾「ターンナップ」. 連立不等式 3x+a＞6x－2, －2x+10≦x+a を満たす実数xが存在するようなaの値の範囲は である。 また、この連立不等式を満たす実数xがちょうど3個であるようなaの範囲は である。 この 2つの所を求める問題ですが、連立不等式の応用さっぱり分かりません。. とりうる値是什么意思_とりうる値是什么意思及发音_日文翻译中文. 沪江日语单词库提供とりうる値是什么意思、とりうる値的中文翻译、とりうる値是什么意思及发音日语翻译成中文、日文翻译中文、日文怎么读、日文怎么写、例句等信息，是最专业的在线日文翻译中文网站 . この時、変数xのとりうる値の範囲をその関数の . 【高校数学Ⅱ】三角関数の最大・最小①（関数の統一・角の統一） | 受験の月. これを2回繰り返すと,sin2θ,の最大・最小に帰着するので, 角2θ,の範囲を確認した上で求める. 高校数学Ⅱ 三角関数. cos36°とsin18°の値（三角方程式を用いた代数的解法）. 定期試験・大学入試に特化した解説。. 三角関数の相互関係や2倍角の公式を用いて . 一次不等式とは？解き方や応用問題（文章題、絶対値や分数） | 受験辞典. 一次不等式とは、 不等式のうち、変数の次数が 1 次（1 乗）の不等式 です。. 例えば、「 x + 1 > 0 」のような不等式です。. 不等式. 左辺と右辺が <, >, ≤, ≥ などの不等号で結ばれた、大小関係を示す式。. 不等式に含まれる変数（ x など）の値の範囲を . 冷やし中華 に 合う 献立

ご 愁傷 様 で ご ざいましたx≧0,y≧0、x+y=4のとき、xのとりうる値の範囲を求め. - Yahoo!知恵袋. x≧0,y≧0、x+y=4のとき、xのとりうる値の範囲を求めよ。 また、x^2+y^2の最大値、最小値と、そのときのx,yの値を求めよ。 . 数学の問題で、 2x + y = －6 x + y = 9 を連立方程式で解く問題なのですが、 問題集の解説を読んでもよく分からなかったのでできるだけ . 【東大数学分野別解説】#14 アプローチが分かれやすい "ベクトル". 2022.03.03. 数学. 東大. 林俊介. この連載では，東大数学の過去問の中から学びの多そうなものを分野別に解説していきます。. 単に正解を述べるだけでなく，問題を解く際のアプローチや補足事項も添えるので，初見の問題への対応力も磨けることでしょう . 【三角比】取りうる値の範囲の考え方、求め方をイチから解説! - YouTube. 高校数学Ⅰで学習する三角比の単元から「とりうる値の範囲」についてイチから解説しています。★教材のプレゼント★高校メルマガ講座は . word 文字 位置 の 指定 に 誤り が あります

−1＜x＜2,1＜y＜3のとき、5x−3yのとりうる値の範囲. - Yahoo!知恵袋. 思い出そうとすればするほど、実在する名称だったか、自分の妄想なのではないかと 混乱してきました。. それっぽい名称がありましたら、教えて頂けると助かります。. 数学. −1＜x＜2,1＜y＜3のとき、5x−3yのとりうる値の範囲を求めよ。. という問題が . 【動画で解説】3x＋y＝6 のとき，z＝x²＋y² の最小値と，そのときのx，yの値を求めよ，x≧0，y≧0のとき，x²＋y² のとりうる値の . ★説明がわかりやすい!と思っていただけたら「高評価」＆「チャンネル登録」お願いします!★問題一覧 ⇒ ei358 . 不等式のとりうる値を求める問題で、わからないことがあります。 - -. - Yahoo!知恵袋. 不等式のとりうる値を求める問題で、わからないことがあります。 -2<x<5 , -7<y<4のとき、x+yのとりうる値の範囲を求めよ という問題なのですが、先ほど解き方を質問させていただいて、頂いた回答を読むことで解けるようにはなりましたが、 解く際に -2-7<x+y<5+4 としています。. 範囲と代表値 - 中学校数学・学習サイト. 資料の値を大きさの順に並べた時の中央の値を 中央値(メジアン) という。 例 生徒25人の身長の中央値は低い方から13番目の人の値となる(高い方から数えても13番目で同じ)。 生徒数が24人の場合、12番めと13番目の2人の値の平均となる。. 【基本】連立不等式と領域 | なかけんの数学ノート. 連立不等式と領域（2直線）. 次の連立不等式が表す領域を図示しなさい。. 「連立不等式」は、「両方の不等式を満たす」ことを意味しています。. つまり、2つの領域の重なっている部分が答えとなります。. 1つ目の式から y ≧ − x が得られます。. これを . 鋭角三角形になるときのxのとりうる値の範囲 -この問題がチャート式を- 数学 | 教えて!goo. である。. またこの三角形ABCが鋭角三角形になるときのxのとりうる値の範囲は. [ウ]＜x＜ [エ] ア、イ、ウ、エに当てはまるものを入れよ。. ア、イはたぶんなんとかわかりました。. 公式：三角形の成立条件. A-B＜C＜A＋B. を使って. 1＜x＜7となりました。. 実数解がとりうる値の範囲 -0<a<2の範囲で、xについての方程式A：x^2-2- 数学 | 教えて!goo. 0<a<2の範囲で、xについての方程式A：x^2-2ax-2x+2a^2-6=0の実数解がとりうる値の範囲を求めよ。という問題なんですが、解き方がいまいちわかりません。ヒントには「解と係数の関係を利用し図形的に解く」や別解として「aの方程式とみる.